Median eigenvalues of subcubic graphs
Zilin Jiang
Arizona State University
December 7, 2025
Joint work with Hricha Acharya and Benjamin Jeter


Median eigenvalues of subcubic graphs
Subcubic graphs
maximum degree at most 3
Eigenvalues of adjacency matrix
$\lambda_1 \ge \dots \ge \lambda_n$
Median eigenvalues
$\lambda_h = \lambda_{\lfloor (n+1)/2 \rfloor}, \lambda_l = \lambda_{\lceil (n+1)/2 \rceil}$
Hückel Model Theory
| Chemistry | Mathematics |
|---|---|
| Organic molecules | Chemical graphs (connected + subcubic) |
| $\pi$-electron energy levels | Eigenvalues |
| Highest occupied molecular orbital energy | $\lambda_h$ |
| Lowest unoccupied molecular orbital energy | $\lambda_l$ |
| Kinetic stability | $\lambda_h - \lambda_l$ |
Fowler & Pisanski 2010
Computations Most chemical graphs have
median eigenvalues in $[-1,1]$, with single exception
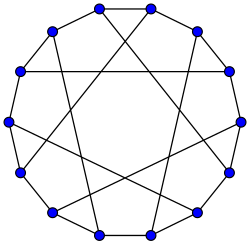
Eigenvalues $-3, (-\sqrt2)^6, (\sqrt2)^6, 3$
Conjecture Median eigenvalues of all but finite chemical graphs are in $[-1,1]$
Optimality
Guo & Mohar constructed infinitely many bipartite chemical graphs with median eigenvalues $\pm 1$
Fowler & Pisanski 2010 Subcubic trees
Mohar 2013 Planar bipartite chemical graphs
Mohar 2016 Bipartite chemical graphs except Heawood
Several other supplementary results
Acharya, Jeter, J., 2025
All chemical graphs except Heawood
Proof
- 1% of proof for 99% of cases
- 99% of proof for 1% of cases
For simplicity, only focus on $\lambda_h \le 1$
Proof for 99%
Take maximum cut $(A, B)$ of $G$
Additional assumption $\lvert A\rvert < \lvert B\rvert$
Observation
Maximum degree of $G[B] \le 1$ and $\lambda_1(G[B]) \le 1$
Cauchy interlacing
$\lambda_{1 + \lvert A \rvert}(G) \le 1$ and $\lambda_h(G) \le 1$
Proof for 1%
Maximum cut $(A, B)$ satisfies $\lvert A\rvert = \lvert B\rvert$
Idea Move $k$ vertices $C$ from $A$ to $B$ s.t.
$\lambda_k(G[B \cup C]) \le 1$
Cauchy $\lambda_{k + \lvert A \setminus C \rvert}(G) \le 1$, and $\lambda_h(G) \le 1$
Note Most of $G[B \cup C]$ are independent edges
Only care about components that contain $C$
Goal Find tail reducer $C$ 🎉
Idea Move $k$ vertices $C$ from $A$ to $B$ s.t.
$\lambda_k(G[B \cup C]) \le 1$
Goal Find tail reducer $C$ 🎉
Note Cut-set of $(A \oplus D, B \oplus D)$
cannot be bigger than that of $(A, B)$
Rule No cut enhancer $D$ 💀
Game
Goal Find tail reducer $C$ 🎉
Rule No cut enhancer $D$ 💀
Lemma If $ab$ is an edge of $G[A]$
then degree of $a$ is $3$ or $\{ a \}$ is tail reducer
Lemma If $ab$ is an edge of $G[A]$
then degree of $a$ is $3$ or $\{ a \}$ is tail reducer
Case 1: $a$ is of degree $1$
Cut enhancer 💀
Lemma If $ab$ is an edge of $G[A]$
then degree of $a$ is $3$ or $\{ a \}$ is tail reducer
Case 2: $a$ is of degree $2$ — $a$ has a neighbor $c$ in $B$
Case 2.1: $c$ has a neighbor in $B$ — cut enhancer 💀
Case 2.2: $c$ has no neighbor in $B$— tail reducer 🎉
Game
Goal Find tail reducer $C$ 🎉
Rule No cut enhancer $D$ 💀
Trick Flip cut preserver ✨
Game
Goal Find tail reducer $C$ 🎉
Rule No cut enhancer $D$ 💀
Trick Flip cut preserver ✨
Levels
Underlying multigraph $M$
Vertices: edges of $G[A] \cup G[B]$
Edges: $k$ edges between $\alpha$ and $\beta$ if $G[\alpha, \beta]$ has $k$ edges
Levels
Underlying multigraph $M$
- $M$ has multiple edges
- $M$ has an isolated vertex
- $M$ contains a $P_5$
- $M$ contains a $C_4$
- $M$ contains a $P_4$
- $M$ contains a $P_3$
- $M$ contains a $P_2$
Statistics
- 24 tail reducers for $\lambda_h \le 1$
- 40 tail reducers for $\lambda_l \ge -1$
- Case 4.4.3.3.3.2.2.2
- 54 pages, 170 figures
Acharya, Jeter, J., 2025
Every chemical graph except Heawood
has median eigenvalues in $[-1, 1]$
All arguments are "local"
Positive fraction $\varepsilon n$ middle eigenvalues $\subset [-1, 1]$
Mohar 2016 Positive fraction for bipartite
chemical graphs except Heawood
Further problems
Guo & Royle 2025 Classified all connected cubic graphs without eigenvalues in $(-1, 1)$
In particular, classified those
with $\lambda_h \ge 1$ and $\lambda_l \le -1$
Problem Classify those with $\lambda_l \ge 1$ or $\lambda_h \le -1$?
Mohar & Tayfeh-Rezaie 2015 Median eigenvalues of every connected bipartite $G$ with maximum degree at most $d$ are in $[-\sqrt{d-2}, \sqrt{d-2}]$, unless $G$ is incidence graph of projective plane of order $d-1$
Optimality of $\sqrt{d-2}$ for $d \ge 4$?
Remove bipartiteness? Mohar $\sqrt{d}$.
Improve to $\sqrt{d-1}$? Improve to $\sqrt{d-2}$?
