Median eigenvalues of subcubic graphs
Zilin Jiang
Arizona State University
June 23, 2025
Joint work with Hricha Acharya and Benjamin Jeter


Subcubic graphs
maximum degree at most 3
Eigenvalues of adjacency matrix
$\lambda_1 \ge \dots \ge \lambda_n$
Median eigenvalues
$\lambda_h = \lambda_{\lfloor (n+1)/2 \rfloor}, \lambda_l = \lambda_{\lceil (n+1)/2 \rceil}$
Hückel Model Theory
| Chemistry | Mathematics |
|---|---|
| Organic molecules | Chemical graphs (connected + subcubic) |
| $\pi$-electron energy levels | Eigenvalues |
| Highest occupied molecular orbital energy | $\lambda_h$ |
| Lowest unoccupied molecular orbital energy | $\lambda_l$ |
| Kinetic stability | $\lambda_h - \lambda_l$ |
Fowler & Pisanski 2010
Computations Most chemical graphs have
median eigenvalues in $[-1,1]$, with single exception
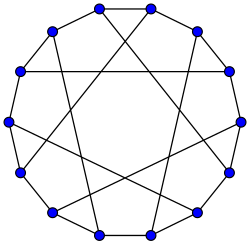
Eigenvalues $-3, (-\sqrt2)^6, (\sqrt2)^6, 3$
Conjecture Median eigenvalues of all but finite chemical graphs are in $[-1,1]$
Optimality
Guo & Mohar constructed infinitely many bipartite chemical graphs with median eigenvalues $\pm 1$
Fowler & Pisanski 2010 Subcubic trees
Mohar 2013 Planar bipartite chemical graphs
Mohar 2016 Bipartite chemical graphs except Heawood
Several other supplementary results
Acharya, Jeter, J., 2025 All chemical graphs except Heawood
- 1% of proof for 99% of cases
- 99% of proof for 1% of cases
For simplicity, only focus on $\lambda_h \le 1$
Proof for 99%
Take maximum cut $(A, B)$ of $G$
Additional assumption $\lvert A\rvert < \lvert B\rvert$
Observation Maximum degree of $G[B] \le 1$,
and $\lambda_1(G[B]) \le 1$
Cauchy interlacing $\lambda_{1 + \lvert A \rvert}(G) \le 1$, and $\lambda_h(G) \le 1$.
Proof for 1%
Maximum cut $(A, B)$ satisfies $\lvert A\rvert = \lvert B\rvert$
Idea 1 Move $k$ vertices $C \subset A$ s.t.
$\lambda_k(G[B \cup C]) \le 1$
Cauchy $\lambda_{k + \lvert A \setminus C \rvert}(G) \le 1$, and $\lambda_h(G) \le 1$
Note Most components of $G[B \cup C]$ are independent edges
Goal 1 Finish with tail reducer $C$
Idea 1 Move $k$ vertices $C \subset A$ s.t.
$\lambda_k(G[B \cup C]) \le 1$
Goal 1 Finish with tail reducer $C$
Idea 2 Cut-set of $(A \oplus D, A \oplus D)$ cannot be bigger than that of $(A, B)$
Goal 2 Contradiction through cut enhancer $D$
Goal 1 Finish with tail reducer $C$
Goal 2 Contradiction through cut enhancer $D$
Lemma If $ab$ is an edge of $G[A]$, then degree of $a$ is $3$, or $\{ a \}$ is tail reducer
54 pages, 170 figures
All arguments are "local"
Positive fraction $\varepsilon n$ middle eigenvalues $\subset [-1, 1]$
Further problems
Mohar & Tayfeh-Rezaie 2015 Median eigenvalues of every connected bipartite $G$ with maximum degree at most $d$ are in $[-\sqrt{d-2}, \sqrt{d-2}]$, unless $G$ is incidence graph of projective plane of order $d-1$
Optimality of $\sqrt{d-2}$ for $d \ge 4$?
Remove bipartiteness? Mohar $\sqrt{d}$.
Improve to $\sqrt{d-1}$? Improve to $\sqrt{d-2}$?
Arizona State University
[email protected]